【Rで機械学習】back queryとムーア・ペンローズ形逆行列の話。

前回の記事、恥ずかしいことに堂々と片手落ちなことを書いてしまっていました。

wanko-sato.hatenablog.com

ニューラルネットワークの出力から入力を逆算するには重み行列の逆行列を用いれば良い、と書きました。
が、これだけでは片手落ちで、逆行列が存在しないケースではこの計算はできないことになります。さすがにそれではいかんと思うので、補足の意味で、逆行列が存在しない場合はどうすれば良いか、メモ書きとして残しておきたいと思います。

そもそも何がだめなのか
逆行列の定義
もう一度見直してみると
一般逆行列
ムーア・ペンローズ形一般逆行列
実験してみよう

そもそも何がだめなのか

ここでは問題の簡略化のため、入力層-隠れ層-出力層のニューラルネットワークを考えます。
入力層から隠れ層への重み行列を $W_{hi}$ 、隠れ層から出力層への重み行列を $W_{oh}$ 、入力ベクトルを $X=(x_{1},x_{2},...,x_{i})$ 、隠れ層の入力ベクトルを $Hi=(hi_{i1},hi_{2},...,hi_{j})$ 、隠れ層の出力ベクトルを $Ho=(ho_{i1},ho_{2},...,ho_{j})$ 、出力ベクトルを $Y=(y_{1},y_{2},...,y_{k})$ と表すことにします。このとき、

$Hi=W_{hi}X$
$Y=W_{oh}Ho$

だったのでした。この式に右側から逆行列を乗じることで、

$\begin{eqnarray} Hi &=& W_{hi}X\\ W_{hi}^{-1}Hi &=& W_{hi}^{-1}W_{hi}X\\ W_{hi}^{-1}Hi &=& IX\\ W_{hi}^{-1}Hi &=& X\\ \end{eqnarray}$

とすることができ、出力から入力を逆算できますよ、ということを前回の記事では述べていました。しかし、そこに前提条件を付けるのをすっかり失念していました。その前提条件とは、「 $W_{hi}$ ならびに $W_{oh}$ の逆行列が存在すること」だったのです。

逆行列の定義

逆行列の定義は

$AB = BA = I$

を満たすn次正方行列が存在するとき、 $B$ を $A$ の逆行列といい、 $A^{-1}$ と表すのでした。赤字で強調したように、逆行列が存在する条件に「正方行列であること」が必要になってきます。

もう一度見直してみると

前回の記事において、back queryを行ったニューラルネットワークのモデルは、入力層、隠れ層、出力層がすべて3つのノードで構成されていました。つまり、重み行列 $W_{hi}$ も $W_{oh}$ も、 $3 \times 3$ の正方行列だったのでした。従って、逆行列が存在する条件がそろっており、特になにも考えずに逆行列を使ったback queryが実行できたのでした。
しかし、一般的なニューラルネットワークにおいて入力層、隠れ層、出力層のノード数がすべて等しいというケースは皆無ですから、逆行列を用いたback queryは「計算上は可能だけれどもほとんど役に立たないもの」になってしまうわけです。それでは意味がないわけで、じゃあどうしましょうか、というところに出てくるのがムーア・ペンローズ形逆行列なわけなのです。

一般逆行列

いきなりムーア・ペンローズ形逆行列の話に入る前に、一般逆行列の話をしましょう。
一般逆行列とは、逆行列が存在しない場合であっても、それっぽい行列を定義してあげて、一般化した逆行列として扱いましょう、というものです。一般逆行列の定義は $m \times n$ 行列 $A$ に対して

$AGA = A$

を満たす $n \times m$ 行列 $G$ のことです。 $m \neq n$ 、つまり行と列の数が異なる、非正方行列でも上記の式を満たす行列がある場合には一般逆行列 $G$ が定義できます。また、 $A$ が正方行列で逆行列 $A^{-1}$ が存在する場合、

$\begin{eqnarray} AA^{-1}A &=& AI\\ &=& A\\ \end{eqnarray}$

となり、一般逆行列の定義式を満たすことがわかります。
ただし、一つの行列に対して一意に定まる逆行列とは異なり、一般逆行列は一意には定まりません。それでは扱いが面倒なので、一意に定まる一般逆行列が必要になります。そこで登場するのがムーア・ペンローズ形一般逆行列、というわけです。

ムーア・ペンローズ形一般逆行列

前置きが長くなりましたが、Wikipediaにも以下のようにある通り、

ムーア-ペンローズの擬似逆行列（ぎじぎゃくぎょうれつ、pseudo-inverse matrix）は線型代数学における逆行列の概念の一般化である。擬逆行列、一般化逆行列、一般逆行列（英: generalized inverse）ともいう。また擬は疑とも書かれる。

一般逆行列といえばムーア・ペンローズ形逆行列のことを指すことが多いようです。
ムーア・ペンローズ形逆行列は、 $m \times n$ 行列 $A$ に対して

$AGA = A$
$GAG = G$
$(AG)' =AG$
$(GA)' = GA$
※'は転置行列を示す

の4つの式を満たす $n \times m$ 行列 $G$ として定義され、記号 $A^{+}$ で表されることが一般的です。この条件を満たす行列は一意に定まるため、逆行列のように扱いやすいものになります。

その他の詳しい説明は

zellij.hatenablog.com

こちらが非常にわかりやすいです。

実験してみよう

モデルの変更

前々回に作ったニューラルネットワークは、入力層、隠れ層、出力層のいずれも3ノードで構成されたものでした。
コードはこちらを参照してください。

wanko-sato.hatenablog.com

入力データは

f:id:wanko_sato:20171001133439p:plain

3次元空間上に正規分布する三色団子でした。つまり、入力は座標データで、出力は3つのグループのいずれに属するか、の確率だったのでした。ここから、単純に出力層のノード数を変えるとしたら、グループを二つに減らせば良いわけで、

#####################################################################################
# create inputData
inputData <- lapply(seq(1,100000),function(i){
  x <- floor(runif(1,min=1,max=3))
  outVec <- c(rnorm(n=3,x*10,sd=3),x)
  return(outVec)
})
inputData <- do.call(rbind,inputData)
for(i in 1:3){
  inputData[,i] <- inputData[,i] - min(inputData[,i])
  inputData[,i] <- (inputData[,i]/(max(inputData[,i])) * 0.99) + 0.01
}

rgl::plot3d(inputData[,1:3],col=inputData[,4])

f:id:wanko_sato:20171126141628p:plain

これでOKです。テストデータも同じように作ってあげれば良いです。
今回は入力層のノード数は3のまま、隠れ層と出力層のノード数を2として、学習を行ってみました。その結果、

f:id:wanko_sato:20171126142107p:plain

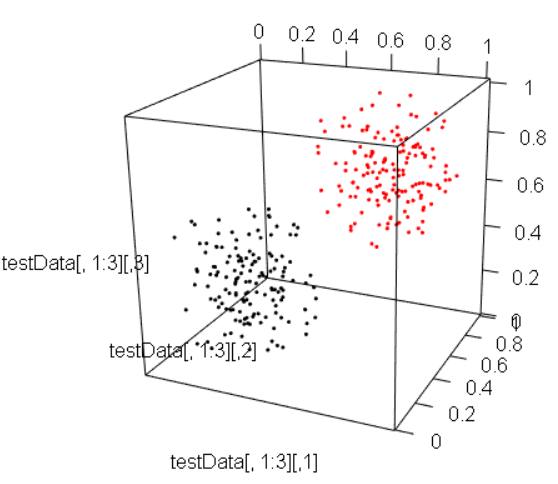
誤識別率0と100％正しく識別できました。このときの重み行列は

> Whi
           [,1]      [,2]       [,3]
[1,]  1.0229319  1.271559  0.6890379
[2,] -0.7156499 -1.141748 -1.1105116
> Woh
          [,1]      [,2]
[1,] -4.406121  19.07303
[2,]  4.449268 -19.26777

となりました。

Rで一般逆行列を計算する

これはとっても簡単で、MASSライブラリを使って

> MASS::ginv(Whi)
          [,1]       [,2]
[1,]  1.157893  0.8852239
[2,]  0.585473  0.1918146
[3,] -1.348125 -1.6681630
> MASS::ginv(Woh)
          [,1]      [,2]
[1,] -549.1463 -543.5962
[2,] -126.8076 -125.5779

これでOKです。

ムーア・ペンローズ形逆行列を使ったback query

特にごちゃごちゃ考えず、テストデータの出力値を入力値とした場合にきちんと入力値が得られるかどうか試してみましょう。
ひとつだけ注意するならば、隠れ層から出力層に与えた値はロジスティック関数を通したものなので、戻すときはロジット関数を通す必要があることくらいでしょうか。それについては前回の記事で紹介しているのでだいじょうぶと思います。

まず一つのデータで実験してみましょう。

> testData[1,1:3]
[1] 0.4487166 0.2237628 0.1041087
> testOut[1,]
[1] 0.96467341 0.03415169

グループ1に属する確率が96.4%と判断されたデータです。これをback queryしてみましょう。

# test
logit <- function(x){
  log(x/(1-x))
}

outIn <- testOut[1,]
outIn <- try(logit(outIn))
outIn <- MASS::ginv(Woh) %*% outIn
outIn <- logit(outIn)
outIn <- MASS::ginv(Whi) %*% outIn

結果は

> outIn
           [,1]
[1,] 0.33122575
[2,] 0.34454031
[3,] 0.05564889

ずいぶん違うところに配置されましたが、グループ1であることは変わりがないようです。
上記で紹介した記事にあるように、ムーア・ペンローズ形逆行列を用いた場合、必ずしも元の値に戻るとは限りません。ただし、ノルムが最小になる値、つまり「いちばんそれっぽい値」に戻すことはできるようです。
では、テストデータを全部使ってやってみたらどうなるでしょうか。

outInList <- lapply(seq_len(nrow(testOut)),function(x){
  outIn <- testOut[x,]
  outIn <- try(logit(outIn))
  outIn <- MASS::ginv(Woh) %*% outIn
  outIn <- logit(outIn)
  outIn <- MASS::ginv(Whi) %*% outIn
  return(t(outIn))
})

outInDF <- do.call(rbind,outInList)

その結果をプロットするとこうなりました。

f:id:wanko_sato:20171126144614p:plain

少々配置が変わっているようにも見えますが、大きく変わっているようには見えません。こんなところでしょうか。

まとめ

ということで、ニューラルネットワークのback queryを逆行列ではなくムーア・ペンローズ形逆行列で行う実験をしてみました。一般逆行列の性質上、出力値をそのまま入力値に戻すことはできませんが、だいたいの値を得ることは可能です。また、ムーア・ペンローズ形逆行列を用いることで、各層のノード数が異なる場合にも対応できるようになり、back query自体をより一般化することができます。
これくらいできれば、ニューラルネットワークの基本的なところは一通り押さえた感じでしょうか。

この先には畳み込みニューラルネットワーク（CNN）やリカレントニューラルネットワーク（RNN）がありますが、それらはニューラルネットワークの基本をベースに拡張されていったモデルですので、まずはニューラルネットワークの基本を押さえておくことが大事になります。逆に、基本さえ押さえておけばその先のモデルの理解はそこまで難しくはありません。どうぞ、臆せず突き進んでいってください。